The study of chaos theory has been a significant area of research in mathematics and physics, particularly in the context of nonlinear dynamical systems. Chen's system, proposed by Chinese mathematician Shangyou Chen in 1989, is a classic example of a chaotic system. This article aims to analyze the hyper-chaos generated from Chen's system, exploring its characteristics, generation mechanisms, and implications in various fields.
Chen's system is a three-dimensional autonomous dynamical system defined by the following equations:
[ begin{align}
x' &= alpha x - yz,
y' &= xz - beta y,
z' &= xy - gamma z,
end{align} ]
where ( alpha, beta, gamma ) are system parameters. The system exhibits chaotic behavior for certain parameter values, leading to the generation of hyper-chaos, which is a higher-dimensional chaotic attractor.
Hyper-chaos is a term used to describe chaotic behavior in systems with more than three dimensions. It is characterized by the presence of at least one positive Lyapunov exponent, indicating exponential growth of small perturbations, and the presence of a complex attractor with a fractal structure.

The hyper-chaos in Chen's system can be analyzed through various methods, including phase portraits, Lyapunov exponents, and bifurcation diagrams. Here are some key characteristics:




The generation of hyper-chaos in Chen's system can be attributed to several factors:



The study of hyper-chaos in Chen's system has implications in various fields, including physics, engineering, and biology. Some of the applications include:

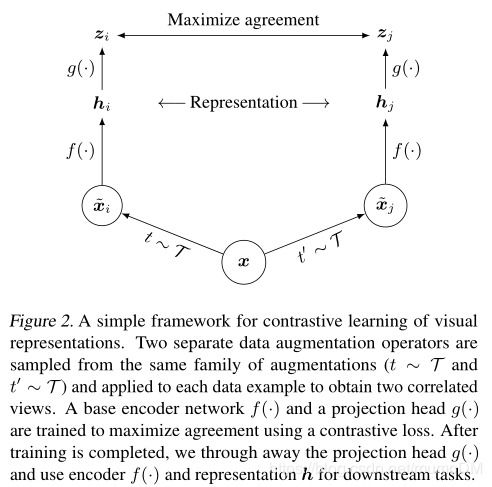
In conclusion, the analysis of hyper-chaos generated from Chen's system reveals a complex and fascinating aspect of nonlinear dynamical systems. The system's ability to exhibit hyper-chaotic behavior highlights the intricate nature of chaos and its potential applications across various disciplines. Further research in this area is essential for a deeper understanding of chaos and its implications in real-world systems.